大きな画面になります
地震のときに倒れたタンスの下敷きになってけがをする人もいます。
あるいは墓石が倒れたことで、どのくらいの力が働いたのか推定する研究もあります。
地震でタンスが倒れないための知識を学びましょう。
非常におおざっぱな話としては、タンスにものがいっぱい詰め込まれていて、
均質だとします。つまりヨーカンを立てかけた状態。
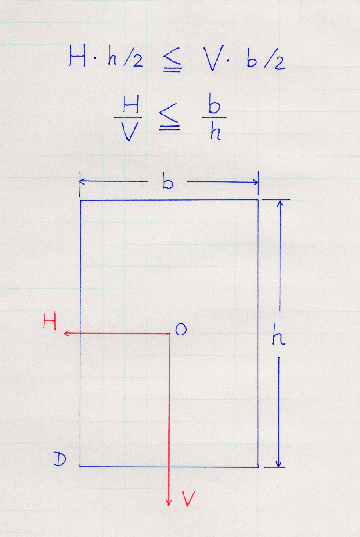
タンスの高さをh、奥行きをbとします。
そうすると重心Oに作用する水平地震力がこのタンスを倒そうとするわけです。
タンスの左下D点に関して転倒させようとする曲げモーメントはH・h/2です。
これに対して、タンスを倒れさせない(抵抗する)力は実は自分の重さに関係します。
つまり、タンスの左下D点に関して抵抗する曲げモーメントはV・b/2です。
ということで、安定するためには
H・h/2 < V・b/2
でなければなりません。
この不等式の符号が逆になったら、タンスは倒れてしまう。
その限界の状態とは H・h/2 = V・b/2
つまり H/V =b/h となります。
経験的には、タンスの奥行きbは高さhの4割以上あれば倒れないとされています。
つまり b/h=0.4
これは H/V=0.4 ということで、地震の力はタンスの重さ(自重)の4割
わかりやすく言えば、地震の力は構造物の自重の4割以下であるということです。
これは経験的には正しいのですが
(私が学生時代に勉強した構造設計では2〜3割の地震力の見積もりだった)、
阪神大震災では場所によっては4割どころか
10割以上もの地震力が働いたので、たいていのタンスは倒れることになってしまいます。
でも、奥行きが高さの4割以上のずんぐりした、いわゆるドラえもん体型のタンス
なら倒れにくいでしょう。
細長いタンスでも下に重い物、上に軽い物を入れておくなら、
重心が下に下がるので転倒に抵抗する力は強くなり安定します。
奥行:高さ=4:10の典型的例「自販機」