地震の時、タンスが倒れないために
　　　　より厳密な理論

さきほどの例では実は地震の上下動を考慮していません。
地震の力が上向きに働けば、一種の浮力のようになって、自重の大きさが減ります。
このような見かけの自重が減ったときにも安定になるよう考えると
次のような理論式になります。

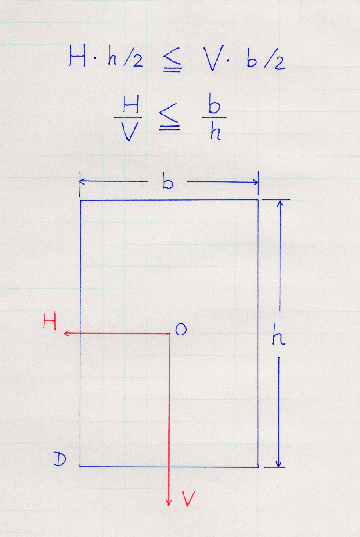
なお、以下に地震力の水平震度をＫ_h、鉛直震度をＫ_vとし
自重をＷとすれば、Ｈ＝Ｗ・Ｋ_h、Ｖ＝Ｗ・Ｋ_vとなります。

大きな画面になります

Ｄ点に関してタンスを左に回転させようとする力はＷ・Ｋ_h・ｈ／２です。
これに対して、元に戻ろうとする力は Ｗ・（１−Ｋ_v）・ｂ／２
ですから、差し引き左回転する力は｛Ｋ_h・ｈ／２−（１−Ｋ_v）・ｂ／２｝Ｗ
となります。
この｛｝の中がマイナスになれば、タンスは倒れないことになります。

さて、実用的にタンスを倒れないよう頂部あるいは底部を固定する場合を考えます。
家具を転倒させる力を上回る固定力は、家具頂部（タンスの右上端）Ｆ_１は
家具底部（タンスの右下端）Ｆ_２よりかなり少なくてすみます。

Ｆ_１≧｛Ｋ_h・ｈ／２−（１−Ｋ_v）・ｂ／２｝Ｗ／ｈ
Ｆ_２≧｛Ｋ_h・ｈ／２−（１−Ｋ_v）・ｂ／２｝Ｗ／ｂ
数値計算として、ｈ＝１８０ｃｍ、ｂ＝４０ｃｍ、Ｗ＝１００ｋｇｆとすれば、
Ｆ_１≧４０ｋｇｆ
Ｆ_２≧１００ｋｇｆとなります。
（ただし　Ｋ_h＝１．０、Ｋ_v＝０．３としたとき）

ただ、このように考えたのは地震力が上向きの時で不利なケースを考えたわけですが、
反対に地震力が下向きになるなら自重が見かけ上増えたことになるから
倒れにくくなるわけです。
したがって、ここで紹介した計算はあくまでも理論的なものです。